SVM(サポートベクターマシン) の SVC(SVM分類) は、ロジスティック回帰と同じように線形に分類するアルゴリズムです。
ですが、「カーネル化」という手法を組み合わせたカーネルSVMを使うことで非線形分離問題にも対応できます。
以前ロジスティック回帰で扱ったXOR分布のデータセットをカーネルSVMで分類しましょう。scikit-learnの sklearn.svm.SVC を使えばカーネルSVMでの分類ができます。
XOR分布のデータセットとは以下のようなデータです。
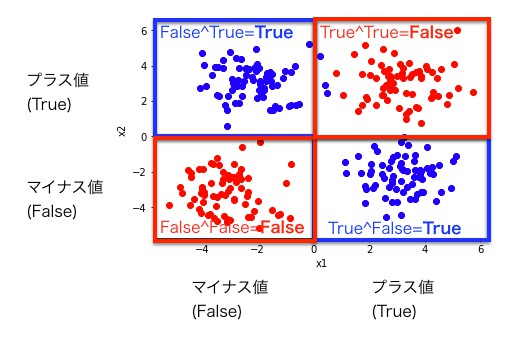
いつも通り、以下の手順でSVMを試してみましょう。
- データの読み込み
- 説明変数(X)と目的変数(y)の取得
- データのプロット
- トレーニング・テスト用にデータを分割
- モデル作成とトレーニングデータの学習
- テストデータでスコア算出
- 学習した領域のプロット
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
def plot_regions(clf, X, y):
X, y = X.to_numpy(), y.to_numpy()
xx1, xx2 = np.meshgrid(np.arange(0, 12, 0.1),
np.arange(0, 12, 0.1))
Z = clf.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=ListedColormap(('red', 'blue')))
plt.scatter(x=X[y == 0, 0], y=X[y == 0, 1], alpha=0.8, c='red')
plt.scatter(x=X[y == 1, 0], y=X[y == 1, 1], alpha=0.8, c='blue')import pandas as pd
# 1. データの読み込み
df = pd.read_csv('./input/data.csv')
df.head(3)# 2. 説明変数(X)と目的変数(y)の取得
X = df.iloc[:, 0:2]
y = df.iloc[:, 2]# 3. データのプロット
plt.scatter(X.x0[y == 0], X.x1[y == 0])
plt.scatter(X.x0[y == 1], X.x1[y == 1]);
from sklearn.model_selection import train_test_split
# 4. トレーニング・テスト用にデータを分割
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)from sklearn.svm import SVC
# 5. モデル作成とトレーニングデータの学習
svm = SVC(gamma='auto')
svm.fit(X_train, y_train)SVC(C=1.0, break_ties=False, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
# 6. テストデータでスコア算出
svm.score(X_test, y_test)0.9916666666666667
# 7. 学習した領域のプロット
plot_regions(svm, X, y);
解説
カーネルSVMも他の分類器と同様に、scikit-learnで簡単に扱えます。
from sklearn.svm import SVC
svm = SVC()
svm.fit(X, y)学習した領域をプロットすると、ロジスティック回帰とは違った非線形な領域が見られます。
このようにSVMは線形非分離な問題も解決できます。
実は前のクエストで、ロジスティック回帰でも線形非分離な問題を解決できると解説しました。
その時はXORデータの軸を掛け算して新しい軸を作って分類しました。
今回のカーネルSVMはそういった処理を自動でやってくれていると考えられます。
逐次自分で軸を追加するのは面倒なのでカーネルSVMを使うと良いでしょう。
サポートベクターマシンでは、同じアルゴリズムで、分類と回帰の2つの機能を使えます。
SVC(Support Vector Classification):分類
SVR(Support Vector Regression):回帰



コメント