非線形なデータをロジスティック回帰で扱う場合

このデータは線形非分離なデータで、ロジスティック回帰では分類できませんでした。このようにデータの傾向により、問題がある場合も一工夫すれば解決できます。解決方法として、x1 * x2の値をとる３次元目の軸を追加して、ロジスティック回帰で分離します。

追加される列new_columnは、内積X.x1 * X.x2で計算できます。
また、np.c_[X, new_column]とすることでXに列new_columnを追加できます。

%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('input/data.csv')

df.head()

# 説明変数Xと目的変数yの取得
X = df[['x1', 'x2']]
y = df['y']

# クラスラベルごとの散布図
X_0 = X[y == 0]
X_1 = X[y == 1]

ax = plt.figure().subplots()
X_0.plot.scatter('x1', 'x2', color='red', ax=ax)
X_1.plot.scatter('x1', 'x2', color='blue', ax=ax);

import numpy as np
new_column = X.x1 * X.x2
extended_X = np.c_[X, new_column]
extended_X.shape

(400, 3)

extended_X[:2]

array([[ 4.46125334,  3.32987675, 14.85542378],
       [ 3.18481539,  1.77078437,  5.6396213 ]])

from sklearn.model_selection import train_test_split

# トレーニングデータ、テストデータに分割
(X_train, X_test,
 y_train, y_test) = train_test_split(
    extended_X, y, test_size=0.3, random_state=0
)

from sklearn.linear_model import LogisticRegression
# ロジスティックモデルの作成
lr = LogisticRegression(C=100, solver='liblinear')

# トレーニングデータの学習
lr.fit(X_train, y_train)

LogisticRegression(C=100, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='auto', n_jobs=None, penalty='l2',
                   random_state=None, solver='liblinear', tol=0.0001, verbose=0,
                   warm_start=False)

# トレーニングデータの学習
lr.fit(X_train, y_train)

LogisticRegression(C=100, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='auto', n_jobs=None, penalty='l2',
                   random_state=None, solver='liblinear', tol=0.0001, verbose=0,
                   warm_start=False)

# スコアの計算
lr.score(X_test, y_test)

1.0

3次元目の軸を追加することで、分類できました（正解率1.0=100%)。

3Dでプロットすると鞍型（くらがた）のデータになります。
追加した軸（下図で縦の軸）は、元の平面に垂直な軸になります。

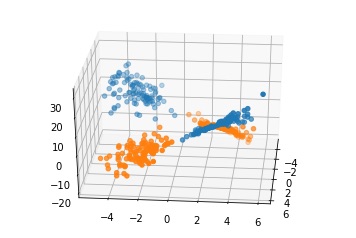
この図を見ると、追加した軸がゼロになる面で区切るとデータはキレイに分割できそうです。
ロジスティック回帰もこれに近い面で分類します。

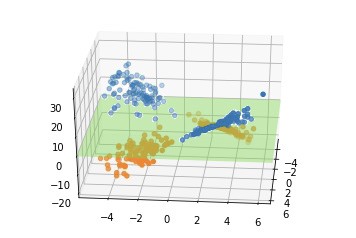
なぜこのような形になるかは、各象限のプラスマイナスに注目すると分かりやすいです。
掛け算の結果、追加した軸は第一、第三象限ではプラスになり、第二、第四象限ではマイナスになります。

第一象限のデータ: x1（プラス） * x2（プラス）
第二象限のデータ: x1（マイナス） * x2（プラス）
第三象限のデータ: x1（マイナス） * x2（マイナス）
第四象限のデータ: x1（プラス） * x2（マイナス）

SVM（Support Vector Machine:サポートベクターマシン）という手法は、このような分類を自動で処理します。今後のクエストで学習しましょう。