回帰分析を使うと、過去のデータから将来を予測できます。
%matplotlib inline
import pandas as pddf = pd.read_csv("input/boston.csv") # ボストン市の住宅価格データ一式
# 予測の対象になる多次元のデータ
X = df.iloc[:, :-1]
# 予測の元になる多次元のデータ
y = df.iloc[:, -1]# 説明変数のサイズ
X.shape(506, 13)
# 説明変数の列名
X.columnsIndex(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX',
'PTRATIO', 'B', 'LSTAT'],
dtype='object')
# RMとLSTATだけに
X = X[['RM', 'LSTAT']]# ヒストグラムと散布図
Xy = pd.concat(objs=[X, y.to_frame()], axis=1)
pd.plotting.scatter_matrix(Xy);
# 相関係数
Xy.corr().MEDVRM 0.695360 LSTAT -0.737663 MEDV 1.000000 Name: MEDV, dtype: float64
yは、予測の対象である「各データのボストン市の住宅価格の中央値」です。
yの名前は、MEDVとしていますので、MEDVで参照しているのは、予測対象です。
実は、住宅価格に密接に関連するのは、列RM(住居の平均部屋数)と列LSTAT(給与の低い職業に従事する人口の割合)です。
簡単にするため、説明変数は、RMとLSTATだけ使います。
scatter_matrixでヒストグラムと散布図を確認します。
pd.concat(objs=[X, y.to_frame()], axis=1)は、Xにyを列MEDVとして追加した表です。
DataFrame.corrメソッドで相関係数の行列を計算できます。行列のMEDV列を取れば、目的変数MEDVと各説明変数との相関がわかります。
この後の問題で、Xを使って、yを予測していきます。
実務では、データを読み込んだら、欠損値の確認や処理、外れ値の確認などの前処理が必要になります。
ここでは、既に考慮済みとして、回帰分析をすることにします。
モデルの評価方法
%matplotlib inline
import numpy as np, pandas as pd, matplotlib.pyplot as plt
from sklearn.metrics import r2_score, mean_squared_error
from sklearn.model_selection import train_test_split
np.random.seed(0) # 写経と同じ表示にするため
df = pd.read_csv("input/boston.csv") # ボストン市の住宅価格データ一式
X, y = df[["RM", "LSTAT"]], df["MEDV"]# 決定係数と平均二乗誤差を計算用に予測データ(y_pred)をダミーで作成
# 下記の式自体に意味はありません(何らかの値が入っていると考えてください)
y_pred = y + np.random.randn(len(y)) * 3def scatter(y_pred, y):
plt.gca().set_aspect('equal', adjustable='box') # 縦横比を1
plt.ylabel('y_test(true)')
plt.xlabel('y_pred')
plt.plot([y.min(), y.max()], [y.min(), y.max()]) # 斜め45度の青い線
plt.plot(y_pred, y, '.')# 決定係数を計算
score1 = r2_score(y, y_pred)
score1# 平均二乗誤差を計算
score2 = mean_squared_error(y, y_pred)
score28.899381155543294
# トレーニングデータとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)- 決定係数(R2, R-squared, coefficient of determination):決定係数は、モデルの当てはまりの良さを示す指標で、寄与率とも呼ばれます。1に近いほど良いといえます。
- 平均二乗誤差(mean square error; MSE):推定値との差分の自乗の平均。最小二乗法では、この基準値を最小化します。小さいほど良いといえます。
- 赤池情報量規準(Akaike’s Information Criterion; AIC):元統計数理研究所所長の赤池弘次先生が考案した統計モデルの良さを評価するための指標。小さいほど良いといえます。
- ベイズ情報量規準(Bayesian information criterion; BIC):AICと同じような統計モデルの良さを評価するための指標。小さいほど良いといえます。
ここでは、決定係数と平均二乗誤差を使うことにしましょう。
決定係数はsklearn.metrics.r2_scoreで、平均二乗誤差はsklearn.metrics.mean_squared_errorで計算できます。
一旦、予測値をダミーで作成してから、練習として決定係数と平均二乗誤差の計算方法を確認します。
また、この後の問題のために、推定値と真値の散布図を表示する関数(scatter)を作成します。
ロジスティック回帰や決定木でやったように、評価するためにはデータを分ける必要があります。
- トレーニングデータ:パラメータの学習に使うデータ
- テストデータ:評価に使うデータ
sklearn.model_selection.train_test_splitでできます。
単回帰
# 前回のプログラムの読込
%run 2.ipynbfrom sklearn.linear_model import LinearRegression
# 出力時に小数点以下3桁に
%precision 3'%.3f'
%precision 3とすると、出力時に小数点以下3桁で表示します。
ただし、NumPyの多次元配列の要素の場合は、この指定が有効になりません。その場合は、float(…)でfloatに変換しています。
# 線形回帰の作成
lr = LinearRegression()
# フィッティング
lr.fit(X_train[['RM']], y_train)
y = intercept_ + coef_[0] * X.RM + 誤差という関係式を考えます。intercept_, coef_は、回帰係数あるいは、回帰モデルのパラメーターと呼びます。
線形(一次式)なので、線形回帰といいます。sklearn.linear_model.LinearRegressionを使います。LinearRegressionでは、最小二乗法という方法で誤差を最小化します。最小二乗法は、平均二乗誤差を最小化する方法です。
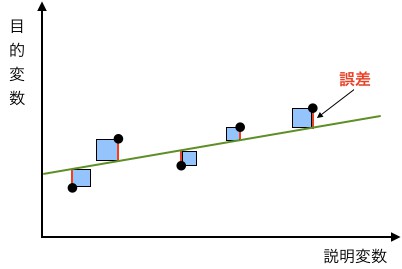
緑の線で表される回帰式と、点で表されるデータとの差が、赤い線で表される誤差になります。
平均二乗誤差は、「誤算の二乗の和/データ数」なので、最小二乗法では「青い正方形の面積の和を最小にする緑の線」を求めます。
回帰分析の手順
機械学習の分類と手順は同じです。
- モデルの作成
- フィッティング(
fit) - 予測(
predict)
# パラメータ(定数項と係数)の確認
float(lr.intercept_), lr.coef_(-36.181, array([9.313]))
パラメータを確認すると、モデルのパラメータは、-36.181 + 9.313 * X.RMになりました。
# 予測値
y_pred = lr.predict(X_test[['RM']])
# 決定係数
score1 = r2_score(y_test, y_pred)
float(score1)0.468
# 平均二乗誤差
score2 = mean_squared_error(y_test, y_pred)
float(score2)43.472
回帰分析の結果の確認
テストデータを使って、予測値(y_pred)を計算します。
- 決定係数は、0.468になりました。
- 平均二乗誤差は、43.472になりました。
予測
# 予測データ(y_pred)と真値(y_test)を描画
scatter(y_pred, y_test)
目的変数から予測値を引いたものを、残差(あるいは誤差)といいます。つまり、回帰分析で予想した直線上の値と、テスト用の値との差です。
散布図で確認してみます。住宅価格が50のところの残差が大きいようです。
# 残差のヒストグラム
plt.hist(y_test - y_pred, range=(-15, 30), bins=45);
残差をヒストグラムでも見てみます。右側の価格が大きい方の裾野が広いのが確認できます。
# 目的変数との残差プロット
plt.hlines(0, 0, 50)
plt.plot(y_test, y_test - y_pred, '.');
モデルの評価において、残差は非常に重要です。
横軸を目的変数や説明変数に、縦軸を残差にした散布図を残差プロットといいます。
良いモデルでは、残差はランダムな成分だけになります。
ランダムな成分だけだと、残差の分布は平均0の正規分布になります。
良いモデルの特徴
- 残差のヒストグラムが、平均が0の正規分布(正規性)
- 残差プロットで、説明変数や目的変数に対して、残差の分散が同じ(等分性)
- 残差プロットで、説明変数や目的変数と残差が無相関(独立性)
上記を満たしていないと、残差の中にまだ情報が残っていることになりますので、モデルの改良の余地があるかもしれません。
重回帰分析
y = intercept_ + coef_[0] * X.RM + coef_[1] * X.LSTAT + 誤差という関係式を考えます。
# 前々回のプログラムの読込
%run 2.ipynbfrom sklearn.linear_model import LinearRegression
%precision 3'%.3f'
# 線形回帰の作成
lr = LinearRegression()
# フィッティング
lr.fit(X_train, y_train)
# パラメータ(定数項と係数)の確認
float(lr.intercept_), lr.coef_(-0.605, array([ 5.018, -0.675]))
# 予測値
y_pred = lr.predict(X_test)
# 決定係数
score3 = r2_score(y_test, y_pred)
float(score3)0.569
# 平均二乗誤差
score4 = mean_squared_error(y_test, y_pred)
float(score4)35.192単回帰分析とモデル(LinearRegression)も手順も同じです。
説明変数として、(2問目で作成したXに含まれる列)RMとLSTATを使います。
- モデルの作成
- フィッティング(
fit) - 予測(
predict)
パラメータを確認すると、モデルのパラメータは、-0.605 + 5.018 * X.RM - 0.675 * X.LSTATになりました。
テストデータを使って、予測値(y_pred)を計算します。
- 決定係数は、0.569になりました。
- 平均二乗誤差は、35.192になりました。
# 予測データ(y_pred)と真値(y_test)を描画
scatter(y_pred, y_test)
- 決定係数を見ると、重回帰分析では全体の56.9%説明できています
- 平均二乗誤差も、重回帰分析の方が小さいので、良くなっています



コメント