モデル式

ボストン市の住宅価格の回帰分析を通して、モデル式を使った回帰分析のモデルについて学習します。
モデル式を使うと、モデルがわかりやすく、修正が容易になります。

モデル式とは、モデルの中から目的変数と説明変数を抜き出して表現したものです。

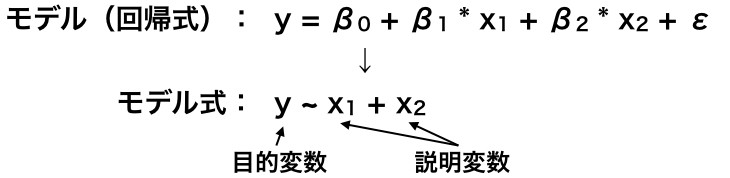
目的変数yと説明変数x1, x2を使うと、モデル式は、y ~ x1 + x2のように表現します。
このモデル式は、y = β0 + β1 * x1 + β2 * x2 + ε（εは誤差）というモデルに対応します。

patsyというライブラリーでモデル式を扱えます。
ここでは、patsy.dmatrixを使って、右辺の説明変数のみ指定します。
目的変数は回帰モデルで指定するので、y ~は記述しません。

%matplotlib inline
%precision 3
import numpy as np, pandas as pd, matplotlib.pyplot as plt
from patsy import dmatrix
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from pandas.plotting import scatter_matrix
pd.set_option('display.precision', 3)  # 小数点以下3桁に

df = pd.read_csv("input/boston.csv")  # ボストン市の住宅価格データ一式

# 説明変数
X = df.iloc[:, :-1]
# 目的変数
y = df.iloc[:, -1]
X[:1]

ボストン市の住宅価格データ（boston）を用います。
13個の説明変数をXに、目的変数をyに入れます。

# 目的変数と各説明変数との相関係数
Xy = X.assign(MEDV=y)  # 目的変数の列MEDVを追加
Xy.corr().MEDV

CRIM      -0.388
ZN         0.360
INDUS     -0.484
CHAS       0.175
NOX       -0.427
RM         0.695
AGE       -0.377
DIS        0.250
RAD       -0.382
TAX       -0.469
PTRATIO   -0.508
B          0.333
LSTAT     -0.738
MEDV       1.000
Name: MEDV, dtype: float64

「目的変数MEDVと13個の説明変数」（Xy）の相関を見てみます。
相関係数の絶対値が0.5以上のものは、RM, PTRATIO, LSTATです。

# 散布図行列を確認
scatter_matrix(Xy[['MEDV', 'RM', 'PTRATIO', 'LSTAT']]);

散布図行列を確認します。

# モデル式から説明変数の表を作成
X1 = dmatrix('RM + PTRATIO + LSTAT - 1', data=X,
             return_type='dataframe')
X1[:1]

	RM	PTRATIO	LSTAT
0	6.575	15.3	4.98

RM + PTRATIO + LSTAT – 1というモデル式から新しく説明変数の表（X1）を作成します。ー1は、y切片を0にするという意味になります。

# 線形回帰でクロスバリデーション
scores = cross_val_score(LinearRegression(), X1, y, cv=6)
score1 = scores.mean()
float(score1)

0.472

線形回帰でクロスバリデーションして、決定係数の平均（score1）を見ます。0.472になりました。

patsy.dmatrixの主なオプション

dmatrixの第1引数は、省略不可で、モデルオブジェクトを指定します。

オプション	デフォルト	説明
data	{}	説明変数のデータ
return_type	‘matrix’	結果の形式

dataには、列名をキーとした辞書相当を指定します。pandas.DataFrameも指定できます。
return_typeを指定しないと、結果がnumpy.ndarrayになります。return_type='dataframe'とすると、結果はpandas.DataFrameになります。