自然言語処理で使われる文書や、画像処理で使われる画像などから生成されるデータは、1サンプルが高次元になることが多いです。高次元のデータは、複雑な処理になったり計算時間がかかったりします。全ての情報が必要かというと、重要性の低い情報も多く含まれています。
次元削減の手法を使うと、有用な情報をなるべく残したままデータ量を削減できます。
ここでは、主成分分析(Principal Component Analysis: PCA)を使って、次元削減してみましょう。
手書き文字を変数dfに変える
まずは、手書き文字の画像を変数dfに読み込みます。dfは、200行×785列の行列データになっており、1行1画像に対応します。
1枚の画像は、縦28ピクセル、横28ピクセル、解像度は8ビット(0から255)のグレースケールです。
1から784列目までは(784=28×28個の)画素データを、785列目は画像が表す数字(ラベル)になっています。
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt# 画像データの読込
df = pd.read_csv('./input/mnist.csv.zip')
df.shape(200, 785)
# 画像の配列としてとりだし
data = df.iloc[:, :-1].to_numpy()
data.shape # 200枚の画像(200, 784)
# 最初の画像(縦28ピクセル x 横28ピクセル = 784画素)
plt.imshow(-data[0].reshape(28, 28), cmap='gray');
df.iloc[行のスライス, 列のスライス]として、スライスで指定された部分行列を取得できます。df.iloc[:, :-1]は、ラベルである最後の列を除いた(784列の)データになります。
DataFrame.to_numpy()で、DataFrameをnumpy.ndarray型として取り出せます。numpy.ndarray型にすることにより、reshapeメソッドが使えるようになります。
-data[0].reshape(28, 28)は、dataの最初の画像データ(data[0])を28×28に変形(reshape)し、白黒反転させるために-1倍したものです。
plt.imshowで2次元の配列データを画像として表示します。オプションcmap='gray'でカラーマップをグレースケールに指定しています。
200枚の画像を重ねて、意味のあるデータの分布をみる
変数dataにサイズ28×28(=784)の画像が200枚入っています。
1枚の画像は、784個の画素からなるデータです。
この画素1つ1つが「0から255の値」を取ります。この1つの画素の値を1つの軸上の値と考えると、784個の1枚のデータは784次元の1つの点に対応するので、784次元と考えられます。
※ 上記の次元は、「NumPyの多次元配列の次元数」ではなく、一般的な次元を意味しています。
しかし、784次元のうち、ほとんどの次元は有用な情報ではありません。
たとえば、1列目のデータは一番左上の画素にあたり、200枚の画像全てで0となっています。
200枚の画像を重ねて、意味のあるデータの分布を見てみましょう。
# 前回のプログラムの読込
%run 1.ipynb
data.shape
(200, 784)# 各画像ごとの一番左上の画素
data[:, 0]array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0])
# 全200枚の画像の重なり
plt.imshow(-data.max(0).reshape(28, 28), cmap='gray');
data.max(0)で、各画素ごとの全200枚の画像の最大値がとれます。
すなわち、200枚の画像の重なった画像として、捉えられます。
この重なり画像は、いびつな楕円であることがわかります。
また、白い周囲の部分は、全列が全て0であることを表しています。
次元の削除
変数dataは、サイズが200×784となっており、784次元のデータが200個あります。
主成分分析という手法を使うと、変数dataを変換して200×Nのサイズの新しいデータを作成できます。Nは分析前に指定した数になります。
次元とは
例:三次元データは、一つのリンゴにたいして、重量、直径サイズ、糖度といったように、三つの観測値があるもののこと。
主成分分析をするとでは(バラツキ)の大きい方向(主成分ベクトルと言います)に沿って、バラツキ具合を変換してデータを取り出せます。下図は2次元平面の場合のイメージ図ですが、変数dataの場合は784次元空間の中に200個の点があることになります。
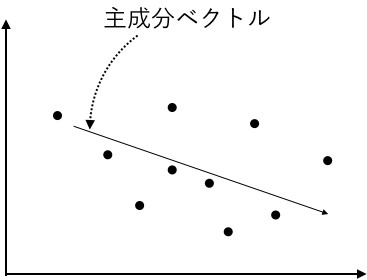
変数dataの主成分ベクトルは、784次元になります。
ここではNを200とします。Nが200なので、784次元のデータを変換すると200次元のデータになります。
一度主成分ベクトルを求めた後、そのベクトルに直交する別のバラツキの大きいベクトルが、次の主成分ベクトルになります。
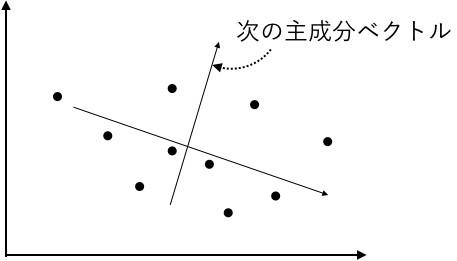
このように主成分ベクトルは、それまでの主成分ベクトル全てと直交するように、最大で空間の次元数までしか求められません(2つのベクトルの間の角度が90度のとき、直交するといいます)。
主成分ベクトル上のバラツキ具合であるデータも、何度も変換できます。
しかし、データが構成する領域も、データ数(画像の枚数)までの次元しか表せないため、最大でデータ数の回数までしか意味のある変換ができません。
つまり、主成分分析で変換できる次元は、元のデータの行数と列数の小さい方までになります。
1枚の画像は784次元ですが、200枚のデータしかないため、
(分類するための)情報量としては200次元分しか使えません。
主成分分析をすると、最大でサイズ200×200のデータに変換できます。
主成分分析のモデル
sklearn.decomposition.PCAが主成分分析のモデルになります。
引数は変換後の次元数で、データの行数(200)または列数(784)の小さい方(200)までしか利用できません。
fit(data)でデータを当てはめ、結果(result)を返します。
result.transform(data)で変換後のデータが得られます。
# 前回のプログラムの読込
%run 2.ipynb
data.shape# 主成分分析で200×784→200×200に変換
from sklearn.decomposition import PCA
N = 200 Nの値を変化させるとN次元数まで削除できる
pca = PCA(N)
result = pca.fit(data) # resultとpcaは同じものです
trans_data = result.transform(data)
trans_data.shape下の解析でも同じ内容。
# 主成分分析で200×784→200×20に変換
from sklearn.decomposition import PCA
pca = PCA(20)
trans_data = pca.fit_transform(data)
trans_data.shape(200, 200)
Nを変化させて次元数を減少させて分類すると、計算時間は短くなりますが精度は悪くなります。実際に次元削減をするときは、精度を確認しながら削減する次元数を変えてみると良いでしょう。
# 最後の変換データ
trans_data[:, -1].round(10)array([ 0., 0., 0., 0., -0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., -0., 0., 0., 0., -0., 0., 0., 0., 0., 0., 0., 0.,
-0., 0., -0., 0., 0., 0., -0., -0., 0., 0., -0., 0., -0.,
0., 0., 0., 0., -0., -0., -0., 0., -0., -0., -0., -0., 0.,
0., -0., -0., 0., -0., 0., 0., -0., 0., -0., -0., -0., 0.,
0., -0., 0., 0., 0., 0., 0., -0., 0., 0., -0., 0., -0.,
0., -0., -0., -0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
-0., 0., 0., 0., 0., -0., 0., -0., -0., -0., 0., 0., 0.,
-0., -0., 0., 0., 0., -0., -0., 0., -0., 0., -0., 0., -0.,
0., 0., 0., 0., 0., -0., -0., -0., -0., -0., 0., 0., 0.,
-0., 0., 0., 0., 0., 0., -0., 0., -0., -0., 0., -0., -0.,
0., -0., 0., 0., 0., 0., -0., -0., 0., 0., 0., -0., -0.,
-0., -0., -0., -0., 0., 0., 0., 0., -0., -0., -0., -0., 0.,
0., 0., 0., -0., 0., -0., 0., 0., -0., -0., 0., 0., 0.,
0., 0., 0., -0., -0., 0., 0., -0., 0., 0., 0., 0., 0.,
0., 0., 0., -0., -0.])
# 1番目の変換データと2番目の変換データの散布図
plt.scatter(trans_data[:, 0], trans_data[:, 1]);
各主成分ベクトルごとの情報量(バラツキ)は、だんだん小さくなります。
trans_data[:, -1].round(10)で最後の200番目の次元を見てみると、ほぼ0となっており、ほとんど情報がないことがわかります。元データは784次元ありましたが、情報としては199次元以下しかないことになります。
round(10)は、小数点以下10桁目で丸めるメソッドです。
plt.scatter(trans_data[:, 0], trans_data[:, 1])で、1番目の変換データと2番目の変換データの散布図を確認しています。
散布図が潰れていないので、十分に情報量(バラツキ)が大きいことがわかります。
主成分ベクトル
結果(result)のcomponents_に主成分ベクトルが入っています。
図で確認してみましょう。
変換したいデータをxとすると、x * 第n主成分ベクトルが変換後の次元がnの値です。
show_image(result, 0)で第1主成分ベクトルを2次元の図として表示します。
手書きのゼロのような形状が見てとれます。
これは、手書きのゼロに近いベクトルを基準にすると、その方向で近い(似ている)ものと遠い(似ていない)ものに分かれてバラツキが大きくなるからです。
# 前回のプログラムの読込
%run 3.ipynb
trans_data.shape# i番目の主成分ベクトルを描画する
def show_image(result, i):
plt.imshow(result.components_[i].reshape(28, 28), cmap='gray')show_image(result, 0) # 第1主成分ベクトル
show_image(result, 1) # 第2主成分ベクトル
show_image(result, 2) # 第3主成分ベクトル
show_image(result, 3) # 第4主成分ベクトル
show_image(result, 4) # 第5主成分ベクトル
show_imageの第2引数を変えていくと、それぞれの主成分ベクトルを観察できます。
数字に近い形状もあれば、そうでない形状もあります。手書きの画像のバラツキによるものと考えられます。
画像の周辺の部分は、情報(バラツキ)がないため、グレー(数値は0)になっています。



コメント