過学習を避けるために

決定木はデータセットに合わせて過度に深くなっています。

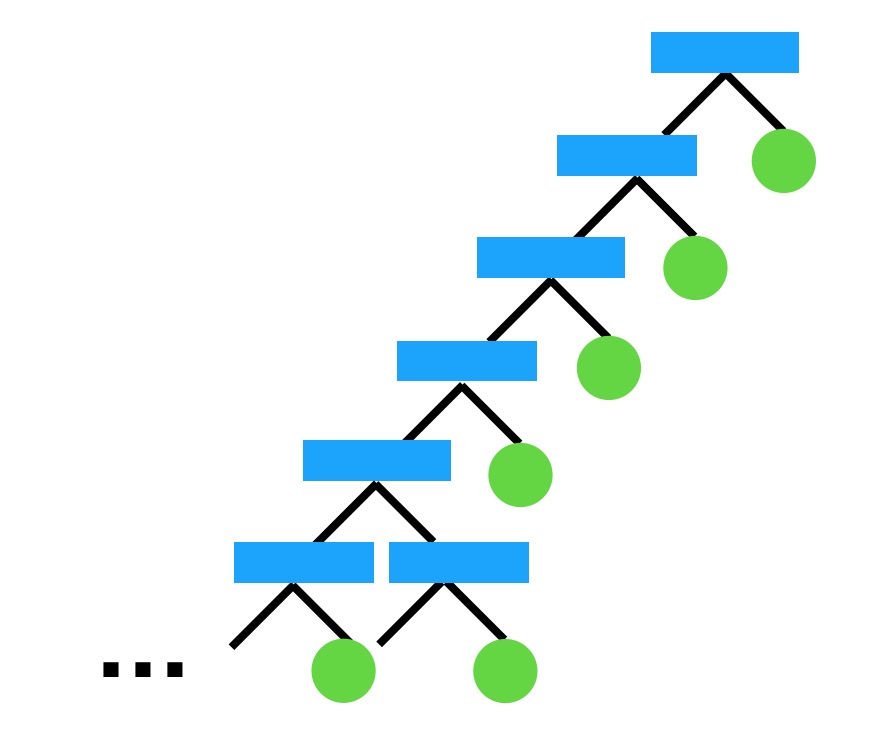
ここでロジスティック回帰のクエストで C= というハイパーパラメーターを指定したことを思い出してください。
ロジスティック回帰のハイパーパラメーターについては、解説で説明します。

LogisticRegression(C=1000, solver='liblinear')

決定木にもロジスティック回帰の C と同じように、ハイパーパラメーターが指定できます。DecisionTreeClassifier にはハイパーパラメーターmax_depthを指定して、決定木の最大の深さを設定できます。

DecisionTreeClassifier(max_depth=3)

max_depth を指定することでその最大の深さが設定できるので、学習時の過度な最適化を制限できます。
たとえば以下の決定木は、最大の深さに 3 を指定した例です。

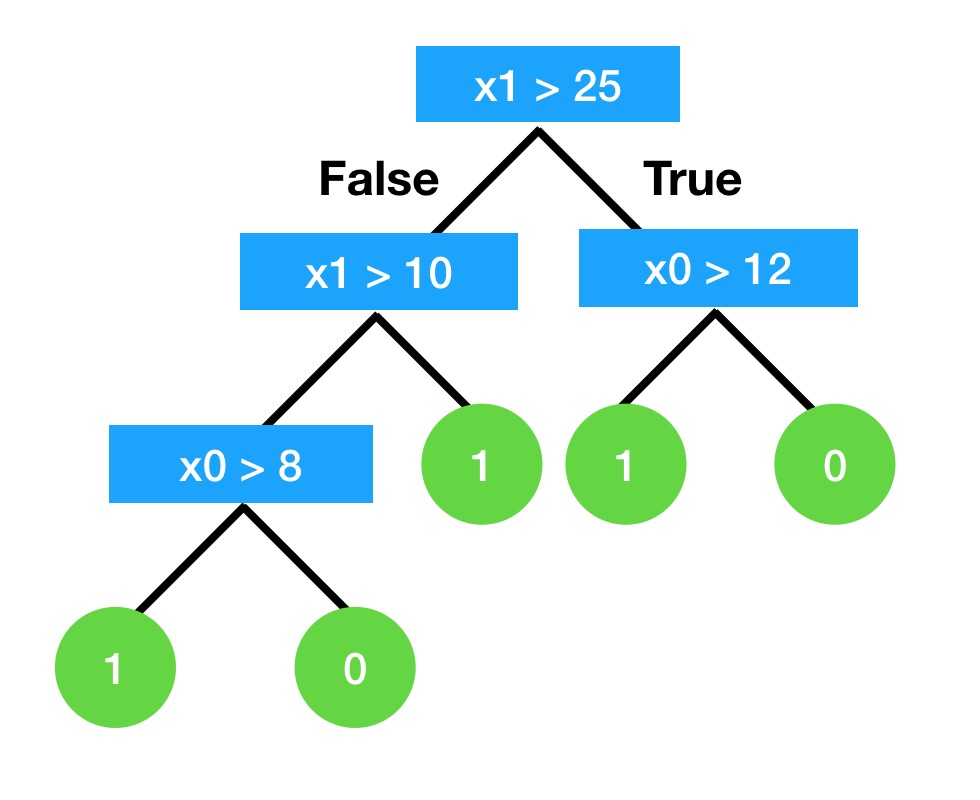
# 前回のプログラムの読込
%run 1.ipynb
df.head()

from sklearn.tree import DecisionTreeClassifier
tree_depth3 = DecisionTreeClassifier(max_depth=3)
tree_depth3.fit(X_train, y_train)

DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion='gini',
                       max_depth=3, max_features=None, max_leaf_nodes=None,
                       min_impurity_decrease=0.0, min_impurity_split=None,
                       min_samples_leaf=1, min_samples_split=2,
                       min_weight_fraction_leaf=0.0, presort='deprecated',
                       random_state=None, splitter='best')

DecisionTreeClassifier(max_depth=3)

DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion='gini',
                       max_depth=3, max_features=None, max_leaf_nodes=None,
                       min_impurity_decrease=0.0, min_impurity_split=None,
                       min_samples_leaf=1, min_samples_split=2,
                       min_weight_fraction_leaf=0.0, presort='deprecated',
                       random_state=None, splitter='best')

tree_depth3.score(X_test, y_test)

0.7592592592592593

plot_tree(tree_depth3, X, y)

tree.score(X_train, y_train)

1.0

tree.score(X_test, y_test)

0.7222222222222222

tree_depth3.score(X_train, y_train)

0.8650793650793651

tree_depth3.score(X_test, y_test)

0.7592592592592593

深さに 3 を指定した決定木で分類しました

DecisionTreeClassifier(max_depth=3)

max_depthを指定する場合の方が正解率も改善していますし、学習した領域をプロットしてみると以前よりも単純な線が引かれることが分かります。

過学習を正解率から見る

トレーニングデータとテストデータでの正答率を比較することで過学習に陥っているかどうかを見てみましょう。

深さ（max_depth）を指定しない場合と、 3 を指定した場合の正解率を比較します。

max_depth を指定しない場合はトレーニングデータでの正解率は高すぎて、テストデータでの正解率が低いです。
これはトレーニングデータに最適化されすぎている、過学習に陥っていると見て取れます。

max_depth に 3 を指定する場合はトレーニングデータでも過度に結果が良すぎることはありません。また、テストデータでの性能も改善しています。
これは過学習ではなくなったと考えられます。

ロジスティック回帰のハイパーパラメーターC

ロジスティック回帰のクエストでCというハイパーパラメーターを設定したことを思い出してください。

LogisticRegression(C=1000, solver='liblinear')

このCは数字が小さいほど過学習に陥りにくくなります。C が小さいほどロジスティック回帰は、各データからわざと距離を置いた場所に分類する線を引こうとします。

わざとこの「ペナルティ」を置くことで、1つ1つのサンプルデータにより過ぎないように学習します。C はそのペナルティの大きさを指定するパラメーターで、大きいほどペナルティは小さくなります。このペナルティを設けることを正則化と呼び、その逆数であるCは逆正則化パラメーターと呼ばれます。